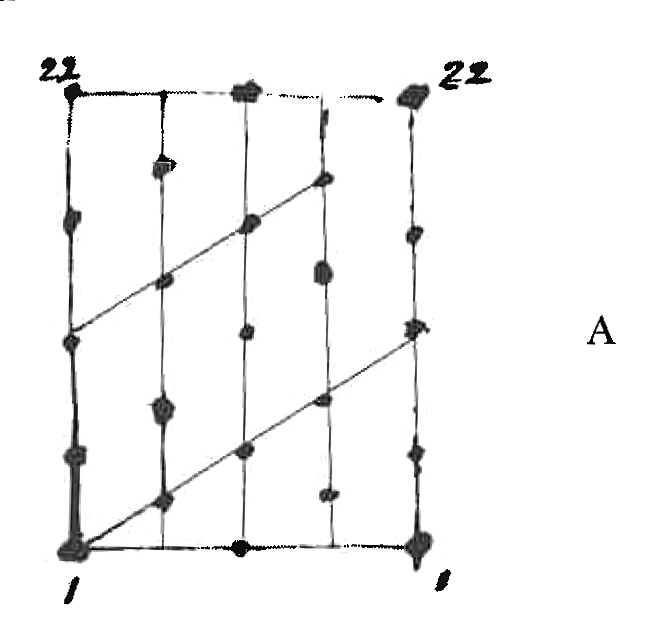
You will see in B that if this cylinder were squashed down flat the spire would become a circle, & then each of the buds would occupy one of the places marked 1, 2 … 21²

Thus Bud 2 would occupy the space betw: 13 & 14   Bud 3 betw: 5, 6; Bud 4 betw: 18, 19. &.c &c & thus every space would be filled but No bud would grow on the top of another. This may be all very old to you, but it was William’s³ suggestion to squash it down & see what happened.

It strikes me as a very neat arrangement

Now if cylinder A were squashed, each bud would be pressed down by a bud above it & it would come to horrid grief ⁴ There are the same No: of leaves in each of these arrangements, if you count 1, & 1 the same & 22 & 22 the same in each.— Turn over.—

B

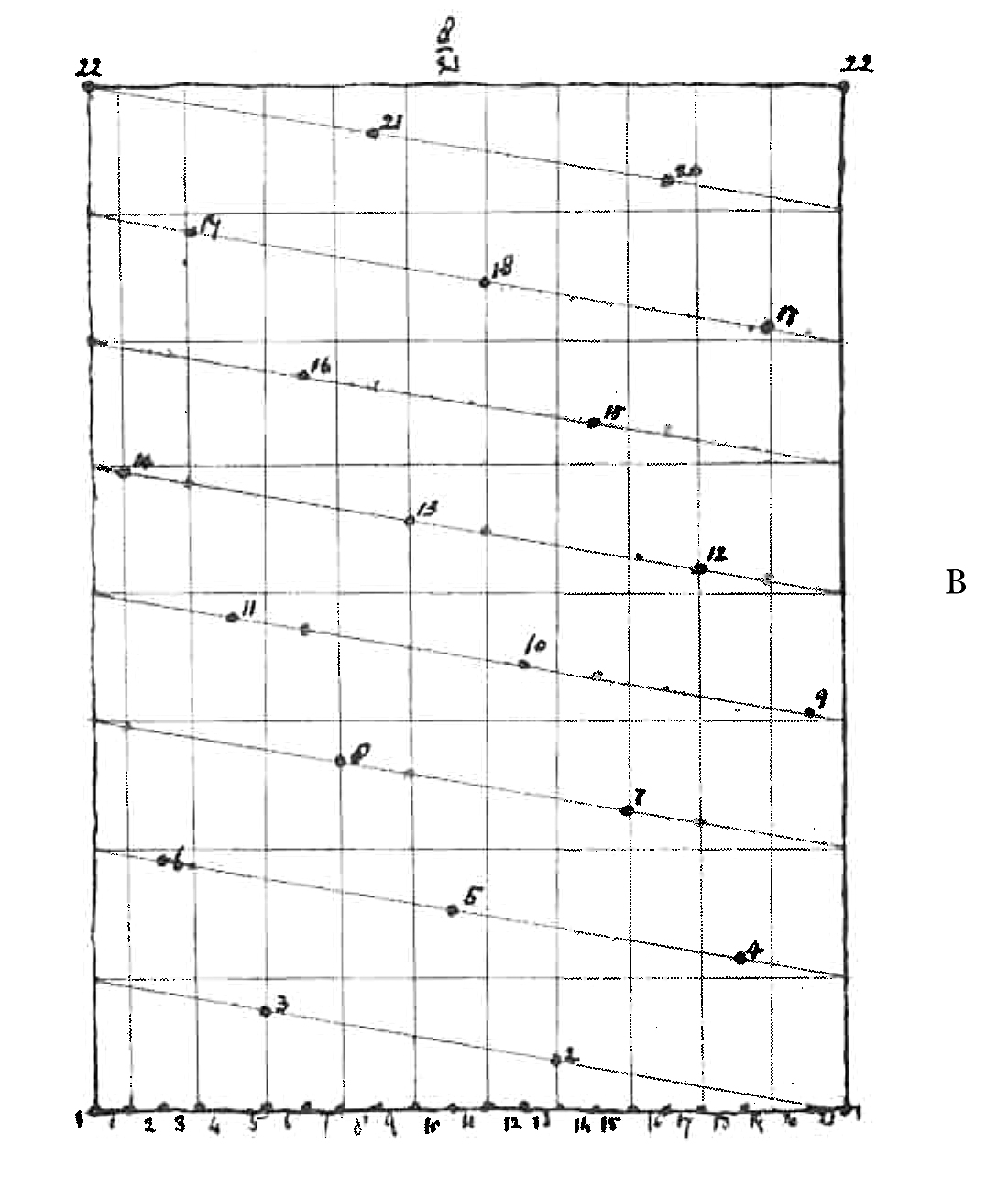
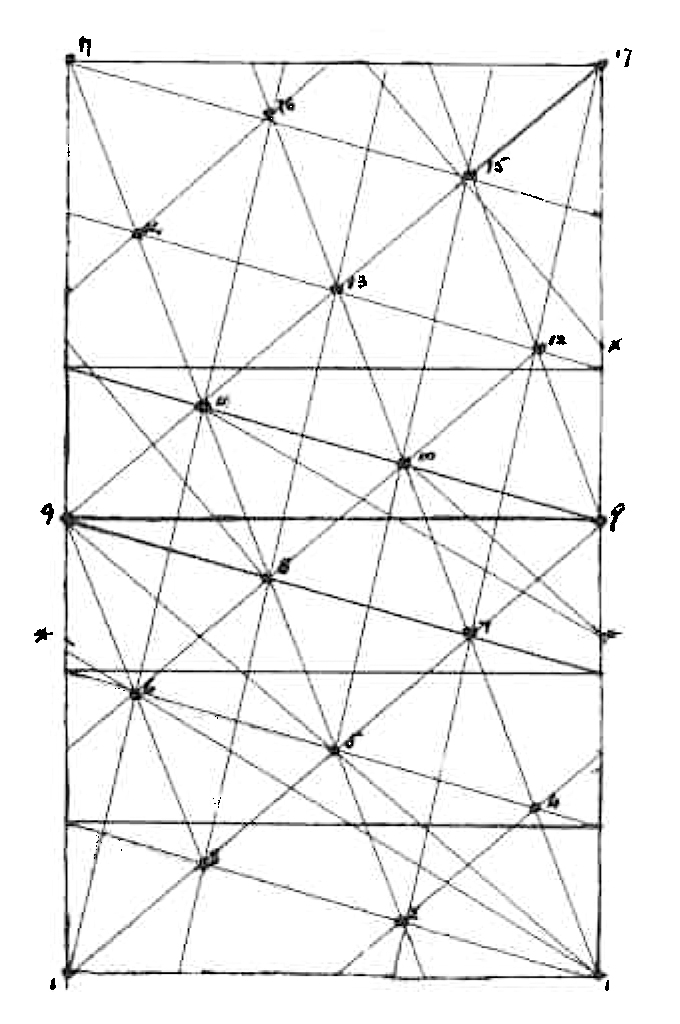
See how strangely one Secondary spire consists entirely of leaves with even numbers & the other with odd numbers.— The worst of it is that these things apply just as well to fractions wh: are not real.

The spires then are

1, 2, 3, .... 1 com: diff:

2, 4, 6, 8 …  2 com: diff:

1, 4, 7, 10 .... 3 com: diff

1, 5, 9, 13 … 4 com: diff

1, 6, 11, 16 … 5 com: diff

1, 7, 13 …  6 com diff

but this is the same spire as

1, 4, 7 &c

1, 8, 15 …  7 com diff:

1, 9, 17— 8 com diff:

this is the same as 1, 5, 9, 13, 17 &.c

&.c &.c

So I suppose there are any no: of spires. ⁵

I’ve come to the conclusion that there are almost any number of secondary spires

for instance 1, 4, 7, 10, 13 &.c

N.B. this is an arithmetical progression with 3 for common difference

1; 1+3=4; 4+3=7; 7+3=10; &.c

again 6, 8, 10, 12 &.c   here 2 is com: diff:

Join 1 (on the left) 8 & 15 & this is another spire. 6

1, 8, 15, &c. here 7 is com: diff: Join 2 & 6 & the line emerges at the * & goes in on the other side at * & then by drawing a line parallel to the old line you pass thro’ 10

thus another is 2, 6, 10

I dont quite understand your question about the cone,⁶ but a piece of paper in this shape 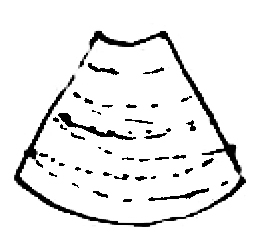if doubled round would form a mathematical cone with the top cut off.

If you look in the other diagram you will see that there you can make as many secondary spiries as you like

I’ve left all those lines in pencil so that you can rub them out.