Darwin Correspondence Project

diagram of your basin if I have understood it rightly, & marked the distances on it. A section passing thro. AF would be an equilateral ▵ and a little bit higher an irregular hexagon 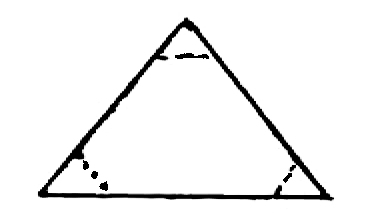[DIAGRAM HERE] with the alternate sides longer and at E it would become a regular hexagon.

I dont think it is possible to draw the intersections of spheres in a simpler manner than the diagrams I return, they are all flat on the paper & real dimensions. If you have 3 spheres only intersecting the central one you will have 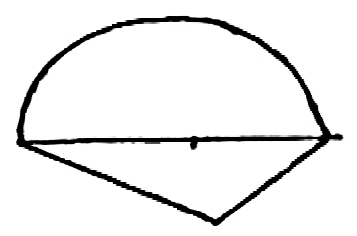[DIAGRAM HERE] 3 semicircles bounded by 12 rhombs, but you cant draw them together with real dimensions as they are in different planes, & their projection would be 3 12 ellipses & 3 foreshortened 12 rhombs. [DIAGRAM HERE]

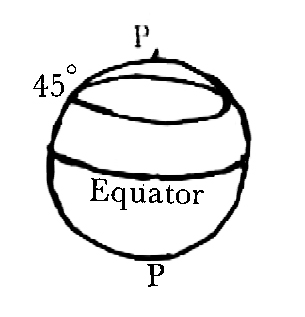
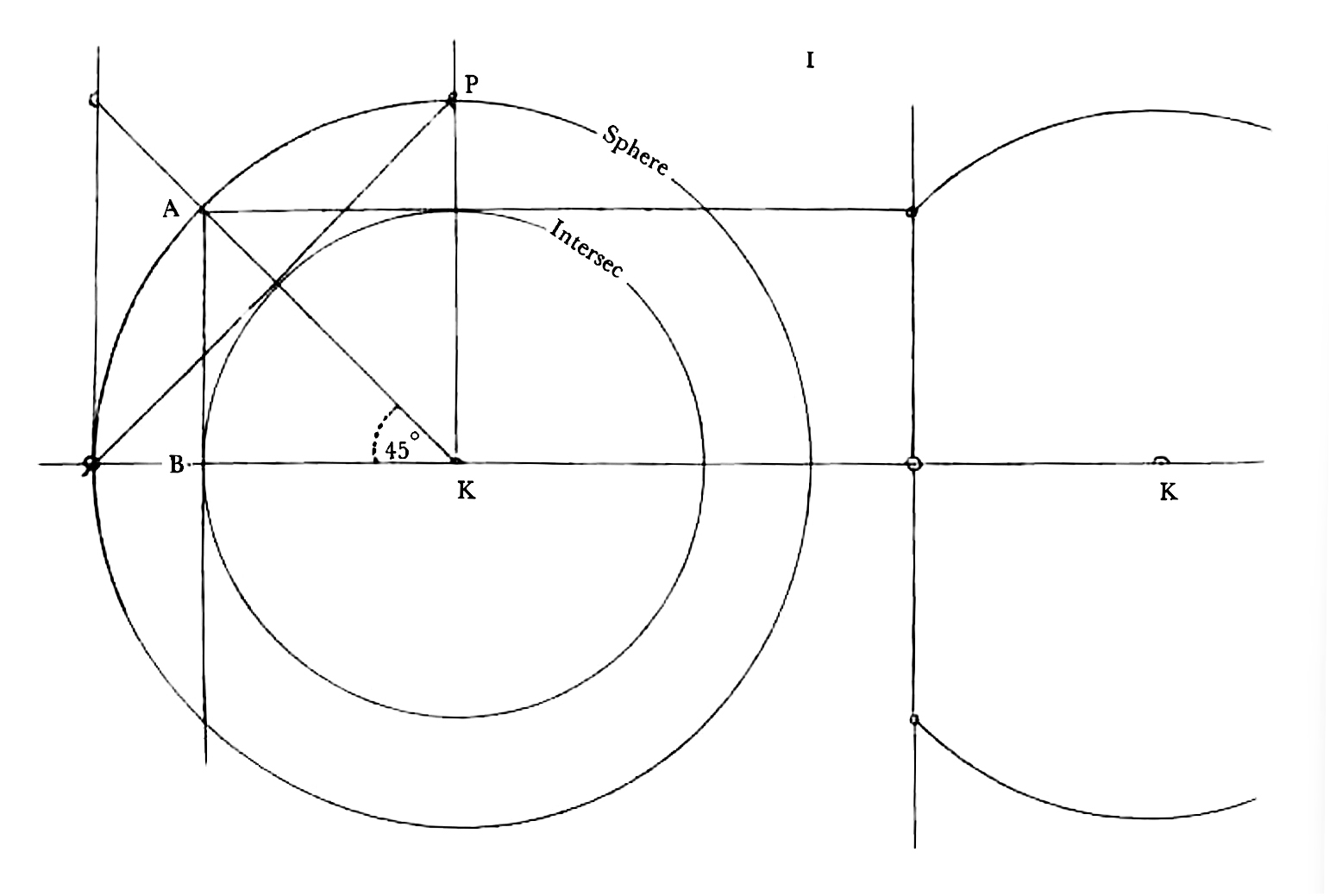
If you take a potato and slice it off at latitude 45^o, you will have the circle of intersection of 2 spheres [DIAGRAM HERE] P 45^o Equator P

You have a deal of trouble before you with carriage & horses worse than Bees cells

E D

[Enclosure 1]}

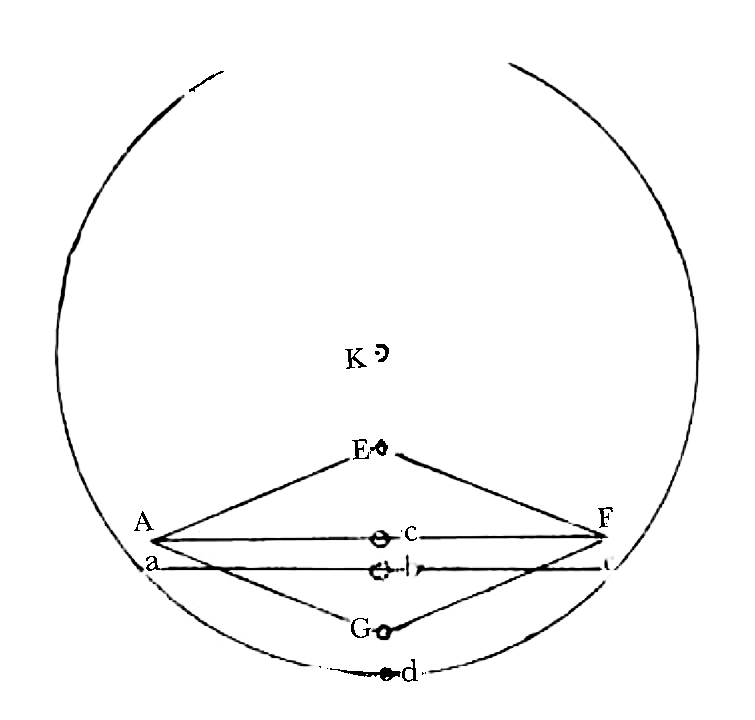
[DIAGRAM HERE] K E A c F a b c G d Rhomb of Bees Dodec linear dimensions magnified 10 times a b c d basin, bd = 0ⁱⁿ05 (real dimension A E F G Rhomb in position, AF or long diameter real dimensions EG short diameter foreshortened cb or vertical heigth to plane of lower ∠^s of rhomb = 0ⁱⁿ01474 in real dimensions

[Enclosure 2]

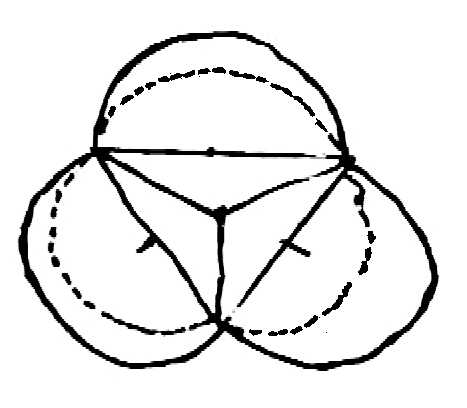
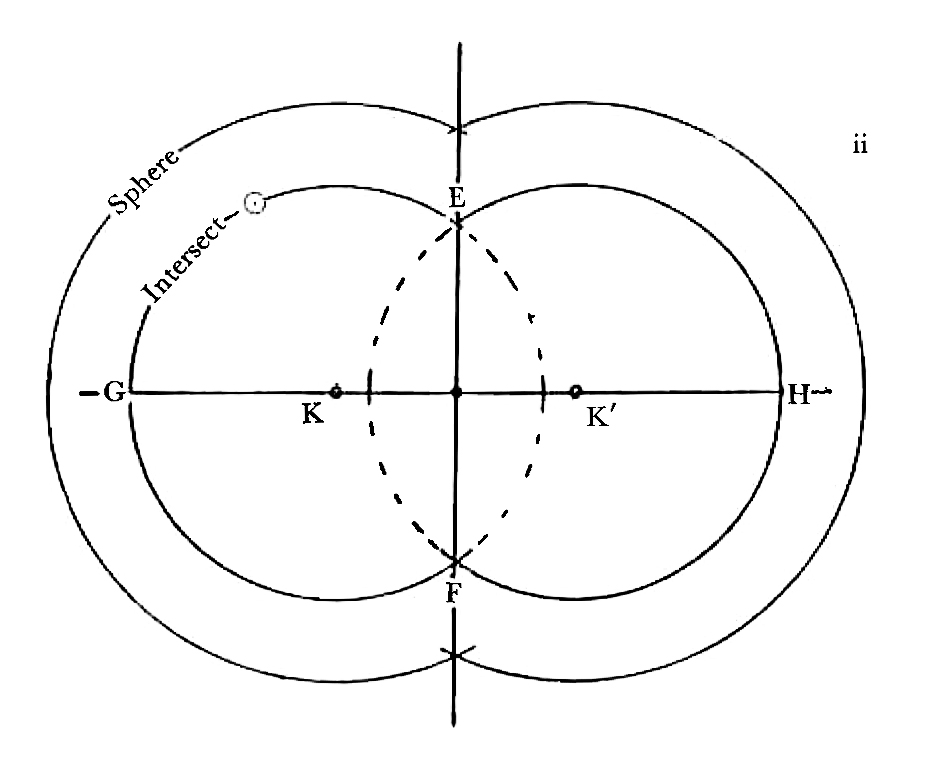
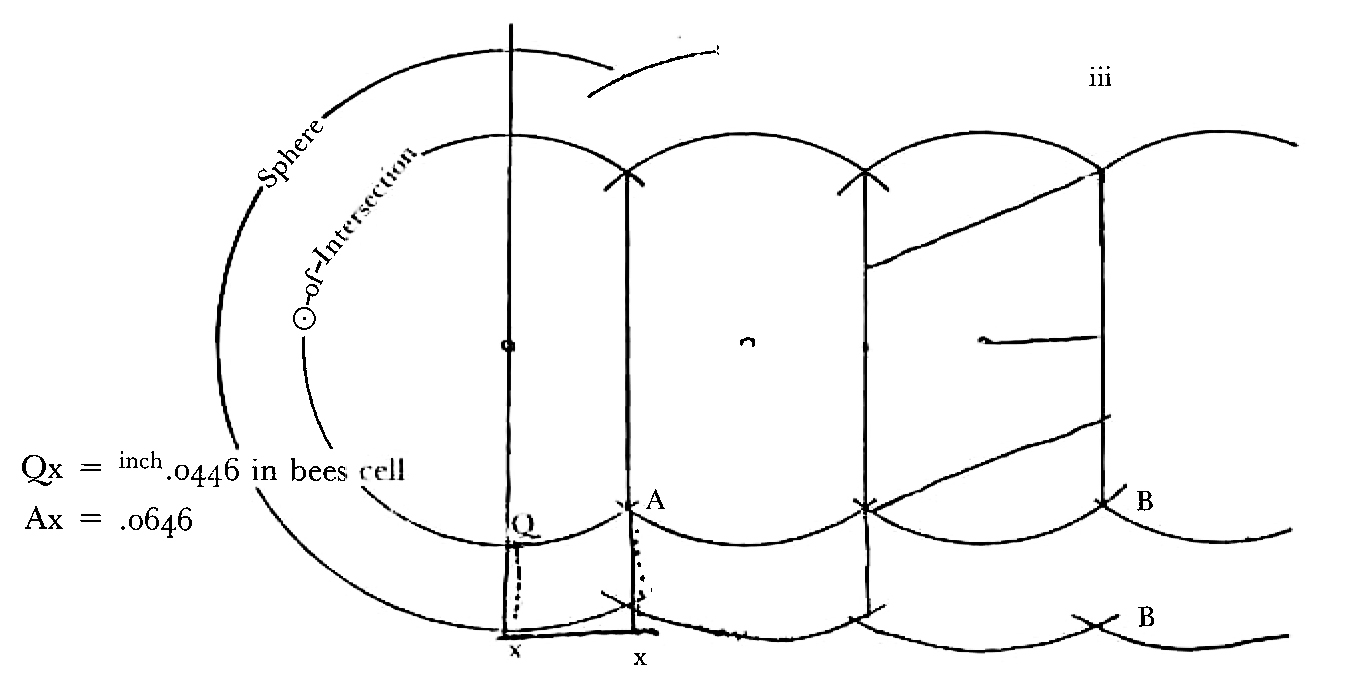
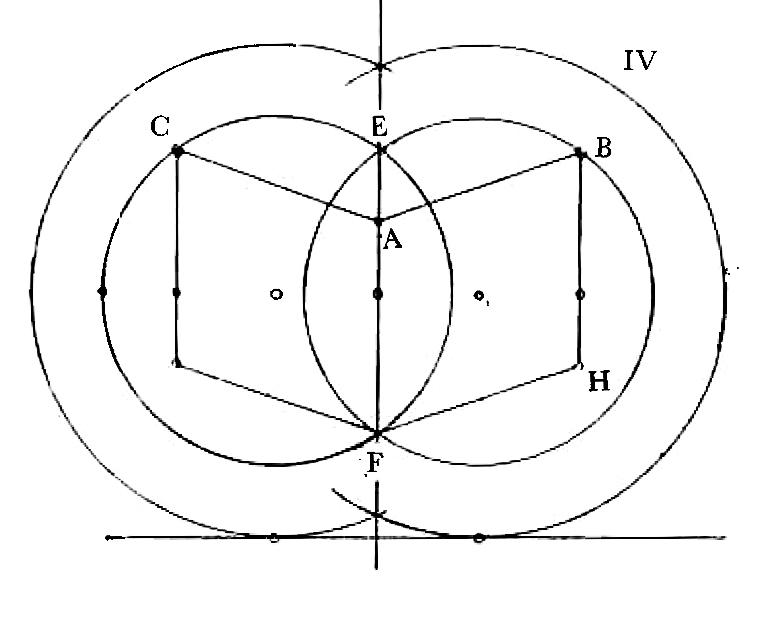
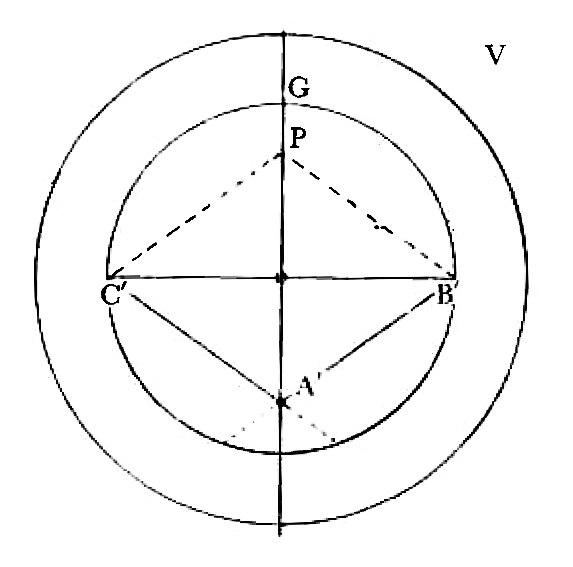
I have drawn you several intersections separately in order not to confuse the drawing & you. I. Projection of ⊙ of intersection parallel to the paper. By way of practise in projections consider your eye to be in the center of one sphere looking at the center of other sphere, or rather looking along the line joining the centers of spheres then the large ⊙ is the projection of both spheres & the small ⊙, the projection of intersection half way. If the intersection plane is perpendicular to the paper then the figure to the right represents it. Or you may consider the circle of intersection to be a parallel of latitude 45^o ii. Two spheres intersecting Then if the 2 circles are inclined to one another at 120^o (∠ of hexagon) the figure will be the ⊙ EHF with part cut off by EF iii a row of spheres the centers all in the same plane IV. Two intersections the same as at iii. If they are inclined at 120^o & a 3^rd sphere intersecting them Imagine V to be so placed that A′ rests upon A, B′ upon B, C′ upon C, then the figure of V will be the semicircle C′GB′ bounded by the half rhomb C′A′B′. Two other spheres with their centers in the same plane as V will cut off the 2 dotted sides of the rhomb The 3 plane ∠^s, CAF, BAF & C′A′B′ form an obtuse ∠ of Dodec, & ABH, A′B′P, form 2 of the plane ∠^s of the acute ∠ of Dodec the other 2 being formed by the adjacent spheres. [DIAGRAM 1] 1 P A B K K Sphere Intersec 45^o [DIAGRAM 2] ii Sphere Intersect ⊙ G K K H F [DIAGRAM 3] iii Sphere ⊙ of Intersection Qx = ^inch0446 in bees cell Ax = .0646 Q A B x x B [DIAGRAM 4] IV C E B A F H [DIAGRAM 5] V G P C' B' A'

ED