From E. A. Darwin [before 8 June 1858]1
Dear Charles.
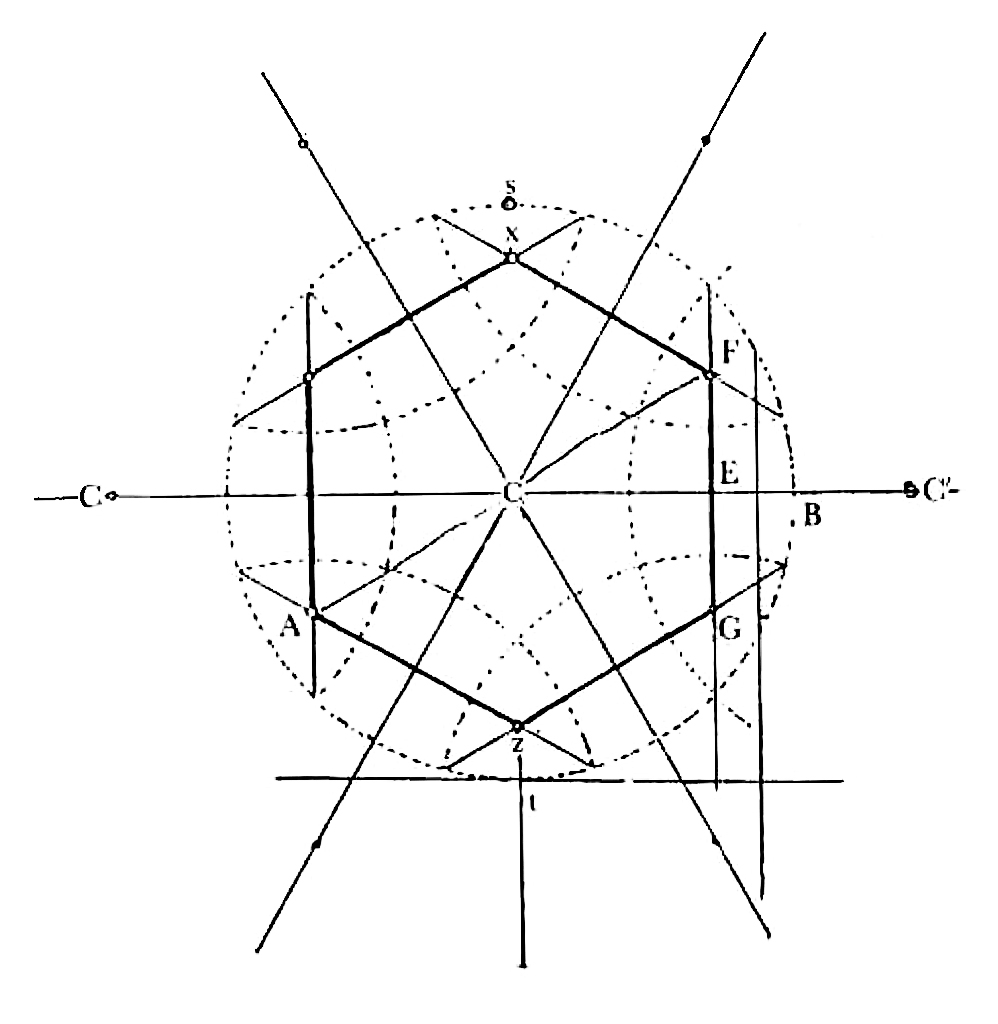
To make sure that I now understand look at my diagram.2 The two
 A, F in the hexagon the section of the Dodec.
A, F in the hexagon the section of the Dodec.
Call CB radius of sphere (r) & CF radius of ⊙ in which the hexagon is inscribed r′, then
| r′ : r :: .8165 : 1 | ||
| in the bees hexagon | r′ = 0inch.125 or ⅛ inch | |
| .:. | r = = = 0inch.153 | |
| r−r′ = 0inch.028 distance sought. | ||
| The distance from center to obtuse ∠ | ||
| = r .866 = 0in.153 ×.866 = 0in.1325 | ||
| distance to ob: ∠ of Dodec | = 0.1325 | |
| r′ = distance to ∠ of Heg | = 0.1250 | |
| Difference = | 0.0075 | |
| or ¾ of inch. | ||
Make no scruple of asking any number of explanations, as it is very little trouble to me, & saves you bother.3
Yours E D
[Enclosure]4
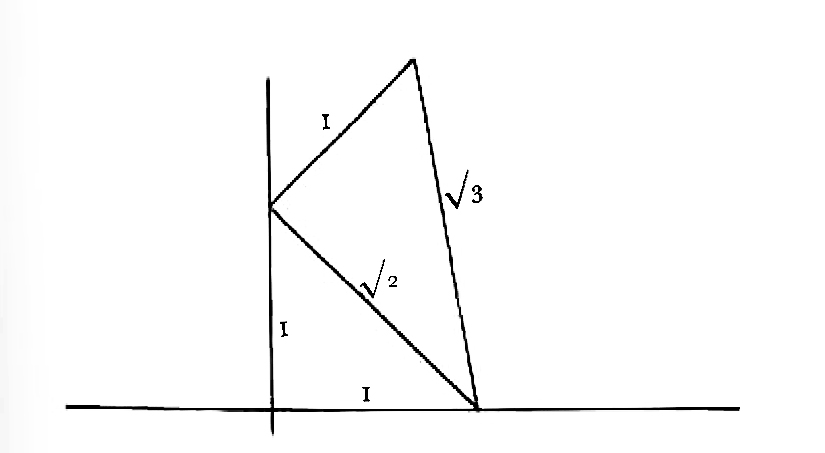
| CB = R = 1 |
|
|
| CC’= R = 1.414 | ||
| EF = FG = side of hexagon | ||
| EF = EC × tang 30o = EC × | ||
| EC = | ||
| 2EF = FG = = .8165 | ||
|
||
CD annotations
Footnotes
Bibliography
Correspondence: The correspondence of Charles Darwin. Edited by Frederick Burkhardt et al. 29 vols to date. Cambridge: Cambridge University Press. 1985–.
Summary
Gives calculations on the structure of bees’ cells.
Letter details
- Letter no.
- DCP-LETT-2278
- From
- Erasmus Alvey Darwin
- To
- Charles Robert Darwin
- Sent from
- unstated
- Source of text
- DAR 162: 48b
- Physical description
- ALS 2pp †, CD note
Please cite as
Darwin Correspondence Project, “Letter no. 2278,” accessed on 19 April 2024, https://www.darwinproject.ac.uk/letter/?docId=letters/DCP-LETT-2278.xml
Also published in The Correspondence of Charles Darwin, vol. 7


